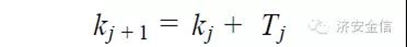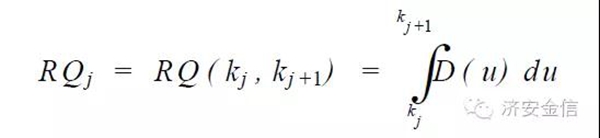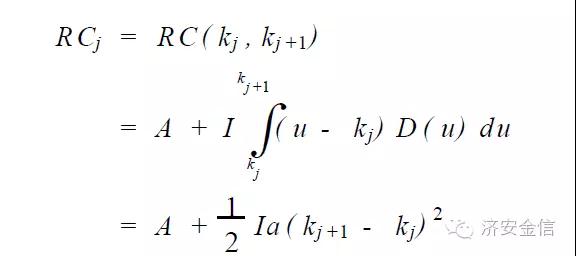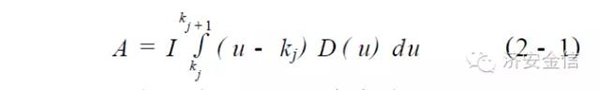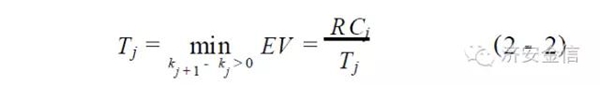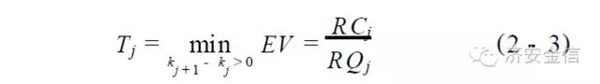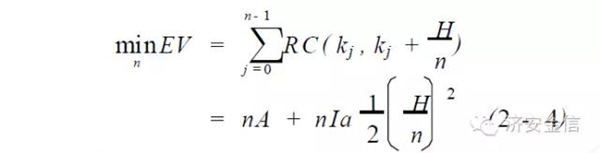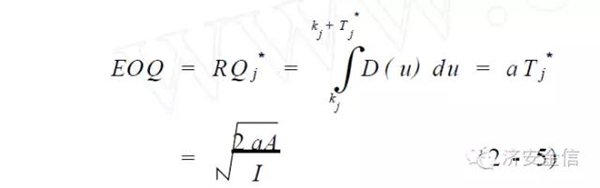【济安管理科学系列】管理科学与管理艺术之统一--杨氏方程(第二章 原始之美)
杨健教授
数学学士、运筹学与经济控制论硕士、
管理科学/运筹学博士(英国兰卡斯特大学)
中国人民大学公共管理定量分析研究所
公共管理学院MPA核心课程首席教授
国家自然科学基金管理科学评审专家
英国运筹学JORS国际顾问委员会理事
二、原始之美:经典EOQ模型
经典的EOQ 问题比较简单,其基本内容是:在商品流通或生产制造的过程中,如果在计划期内,对一类物品的需求率保持不变,管理者应当如何确定订货/ 生产的时间和数量? 在研究EOQ公式变迁的过程中,我们发现了一个殊途同归的奇怪现象,即四类著名的物流管理策略在市场需求不变的条件下,具有和谐的、统一的数学结构。
一般来说,基本参数包括:计划期H ,即更新决策问题的时间范围,通常EOQ 的假设是一年;在时间t 时刻的需求率D ( t ) ,在计划期H 内可以是恒定的常数,也可以是时间的函数;初置成本A是指企业启动生产制造的主要成本,如锅炉预热、生产组织、集装箱运输或订货等费用;单位时间单位物品的存储成本I 蕴涵着与产品的物理属性有关的直接成本和内部结算。
决策变量比较复杂,对于经典的EOQ 问题,订货—生产的更新次数n 相当于决策变量,而对于时变需求, n 相当于一个环境变量;第j 次更新时点kj 是决策变量;当kj 已经确定时, 第j 次与第j + 1 次更新的时间间隔Tj 与kj + 1是等价的决策变量,即
第j 次更新数量RQj 的表述如下:
第j 次更新成本RCj ,则可以表述为:
不失一般性, EOQ 公式的基本假设如下:需求有连续、稳定和已知的速度;前置时间已知且固定;货物补足的作业周期是固定的;货值是固定的,与订货数量和时间无关;仅考虑库存持有成本I 以及每次订货成本A ;库存的各品种间无相互影响;无在途货物; 没有资金的约束。我们注意到,经典的EOQ 问题隐含假设计划期H 是无穷大的,这意味着约束条件kj + 1 = kj + Tj < H 对决策变量Tj 的约束并不成立。因此,单期更新决策与多期更新决策是完全等价的。单期更新决策模型有以下四种:
(1) 美国人Ford W. Harris 于1913 年首先发明了经济生产量EPQ 模型( Economic Production Quantity) ,目的是为了决定生产数量与合理地控制库存。通过平衡订货成本与库存成本, Harris利用一元二次方程求根获得了EOQ 公式。我们在更新决策单元内,建立以初置成本( setup cost )与运营成本(carrying cost ) 的平衡为目标函数的Harris 模型:
(2)几乎同时, EOQ 公式亦由R. H. Wilson不谋而合地发现了,并被作为库存管理方案的一部分出售给了许多公司,因此人们又称之为Wilson 公式。与Harris 的初衷不同,Wilson 公式试图给出最小化单位时间总成本的最佳订货量。我们在更新决策单元内,建立以在单位时间内更新成本最小为目标函数的Wilson 模型:
(3) 今天,在流行的经济管理教科书中都陈列着与当年一模一样的经济订货量EOQ 公式或经济批量模型ELS( Economic Lot Size) ,但是,其决策理念却与以往大不相同,其推导过程是以优化单位物品成本为目标,在无限的计划期的假设下,通过更加现代的微分技巧求出无约束的极值点EOQ。我们在更新决策单元内,建立以物品总量的单位平均更新成本最小为目标函数的CLUC(Continuous Least Unit Cost) 模型:
(4) 令人困惑的是,人们似乎有意地遗忘了开山鼻祖,有人直接根据需求恒定的假设,推知订货数量、更新时间间隔亦为常数。通过直接确定最佳的更新次数,使相当长的计划期内的总成本最小,同样也可以推导出EOQ 公式。虽然在严格意义上整数不能作为求导变量,但是仍然可以作为一种解决问题的途径,正所谓异曲同工! 在相当长的计划期H 内,我们建立以总成本最小为目标的更新次数模型:
不难证明,上述四类更新决策模型虽然各异,但是其最优决策变量T*j 却完全相同,即
究竟是什么原因导致了不和谐的管理决策理念,却在数学模型上殊途同归呢? 经过考证,我们发现, EOQ 世界之所以和谐的原因,依旧是几乎被人们遗忘的固定需求率假设:无论市场环境如何变迁,无论岁月如何流逝,产品的需求量却是永恒不变的。
上一篇:杨氏方程(第一章 发端之美)
下一篇:杨氏方程(第三章 混沌之美)
- 第十九次全国代表大会报告全文2017.10.18
- 中共十九大隆重开幕2017.10.18
- 新三板企业IPO热情高涨 11家已上2017.10.18
- 新一届发审委委员六大看点2017.10.12
- 人民币汇率升值与人民币贬值的两2018.06.15
- 杨氏方程(最终章 统一之美)2018.06.15
最新文章
-
百度料成搭乘CDR“首
中国证券报记者从知情人士处获悉......

-
中国人保IPO过会 拟
6月5日,证监会发审委召开第85次I......

-
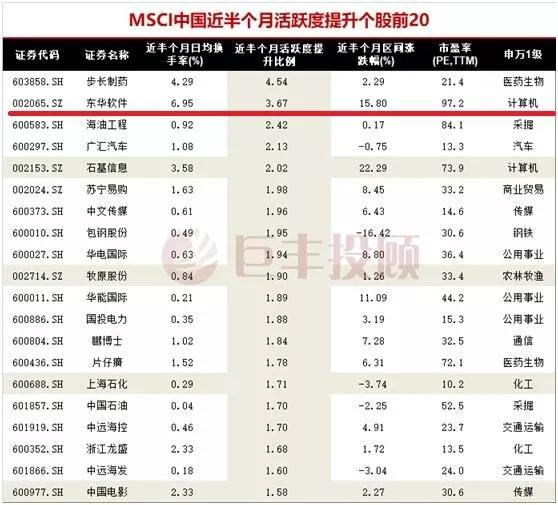
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......
-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

推荐文章
-
百度料成搭乘CDR“首
中国证券报记者从知情人士处获悉......

-
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......

-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

热门文章
-
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......

-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

-
东华软件在2018数博
5月29日,2018中国国际大数据博览......