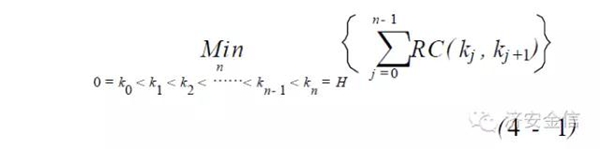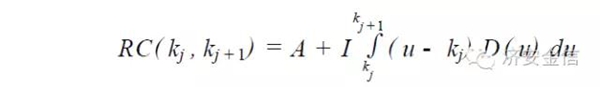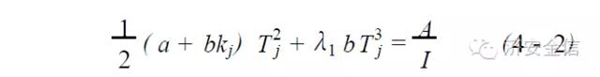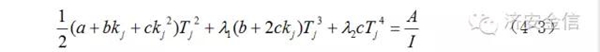【济安管理科学系列】管理科学与管理艺术之统一--杨氏方程(第四章 和谐之美)
杨健教授
数学学士、运筹学与经济控制论硕士、
管理科学/运筹学博士(英国兰卡斯特大学)
中国人民大学公共管理定量分析研究所
公共管理学院MPA核心课程首席教授
国家自然科学基金管理科学评审专家
英国运筹学JORS国际顾问委员会理事
四、和谐之美:解析的启发式算法
每一种产品都有生命周期和季节性波动,其市场需求必然呈现出线性或非线性的变化。当年不同流派的管理科学大师在不经意中埋下了这颗“惹祸的种子”———固定需求率假说,竟然诱发了后人的诸多争议。由于讨论的问题不同、假设不同,导致相关的管理科学理念、模型和算法出现了混乱和分歧。物流管理不和谐的起因正是不断变化的外部市场环境。关键问题在于两方面:一是四大流派的数学模型能否真正统一? 二是解析的启发式算法是否存在?
不失一般性,我们假设动态更新决策问题:
其中,
在运筹学中有约束的物流问题往往很难求解,Florian et al. (1980) 曾经证明几类一般形式的单品种有约束批量问题是NP-hard。
自20 世纪初至今有数百篇涉及EOQ 模型或Lot Sizing 算法的论文,由此足见问题的重要性,而其混乱程度亦见一斑。在科学技术发展过程中,当一种反常现象与通常理论发生冲突时,就会出现理论危机。自然科学的其他领域如数学、物理、化学等都有类似的“科学统一性”质疑和讨论。
为了描述物流管理历史沿革和澄清物流决策模型与算法的类型,更新决策问题一般分为静态批量决策(Static Lot Sizing) 和动态批量决策(Dy2namic Lot Sizing) 。前者主要包括EOQ、EPQ、RC和FOQ 等方法;后者包括三类:简单方法( FixedPeriod ,Period Order Quantity ,Lot for Lot ) 、无约束离散问题的最优算法(Wagner-Whitin) 和启发式算法( Silver-Meal ,Least Unit Cost , Part PeriodBalancing ,Ritchie) 。
对数学工作者而言,一个数学模型的可构造性、数据是否可获得、解析解的存在性、问题的可计算性、算法的准确性和复杂性,以及计算结果是否可解释等基本问题是非常重要的。如果数学模型仅仅是一种对决策理念的描述而无法计算,那么其学术价值就值得商榷了。不同的euristics 就会计算出各自相应的单期更新决策,由此构成的多期更新决策或动态更新决策,对于不同的物流问题其实难分高下。
在需求线性变化时,上升问题和下降问题分别被Yang 与Rand 于1993 年和Zhao 、Yang 与Rand 于2001 年解决了。1993 年, Yang 与Rand证明,如果设定参数λ1 分别为1/ 3 、2/ 3 、1/ 6 和0.43 ,则存在统一的数学结构:
这个方程可以涵盖: (1) 以初置成本与运营成本平衡为目标函数的Harris 模型,即PPB ; (2) 以在单位时间内成本最小为目标函数的Wilson 模型,即Silver-Meal ; (3) 以单位成本最小为目标函数的CLUC 模型; (4) 以在相当长的计划期H 内总成本最小为目标的Ritchie 模型,即企业长期发展策略对应于计划期H 趋于无穷大的“百年老店”。如果参数λ1 遍历[ 0 ,1 ]区间,则可获得非常理想的更新决策,至少优于上述四种算法。
在需求二次非线性变化时,1999年Yang、Zhao和Rand首次证明了如果设定参数向量(λ1 ,λ2 )分别为 (1/3, 1/4)、(2/3, 3/4)和 (1/6, 1/12),则由统一的代数方程
可以成功地获得对应上述三种不同决策策略的数学模型。令人遗憾的是,最后一种“百年老店”的情况仍在证明过程之中。根据这个方程设计出的解析算法YZR 亦非常出色,作为应用特例,我们首次给出了上述三种物流管理策略的相应解析算法,使准确地对它们进行比较研究成为可能。
Yang-Zhao-Rand 算法是目前准确无误地获得Part Period Balancing 模型、Silver-Meal 模型和Least Unit Cost 模型的动态更新决策{ kj} 的惟一途径,被称为是“当今众所周知最好的启发式算法之一”,其引入的12 个非线性问题则作为“经典算例”被同行多次引用。
启发式算法的要义是“具体情况,具体分析”。上述方程蕴涵了清晰的更新决策理念、优美的数学结构和简捷的解析算法,展现了管理科学的和谐与统一。“和谐之美”的价值不仅在于其在数学上提供了当今最好的解析算法,而且在于其为物流管理找到了更新决策的一般规律。
对管理科学而言,发现具有一般性的代数方程之意义不仅在于找到了一个世界上最优秀的启发式算法,而且在于其方程中的参量(λ1 ,λ2) 本身具有探询最佳管理策略的定向功能:根据最佳参量(λ*1 ,λ*2 ) , 可以追溯到理想的管理境地, 为经理们在物品所处的市场环境中找到其生产制造和订货的最佳策略。例如,在二次非线性需求的条件下,如果最佳参量(λ*1 ,λ*2 ) 接近于(1/ 3 , 1/ 4) ,则以均衡生产、订货和库存之平衡为操作理念坚持运营成本与订货成本相匹配的准则;如果最佳参量(λ*1 ,λ*2 ) 接近于(2/ 3 , 3/ 4) ,则以稳健财务为核心坚持现金流管理;如果最佳参量(λ*1 ,λ*2 )接近于(1/ 6 , 1/ 12) ,则管理策略应当以需求为导向,坚持核算最小单位成本。对于具体的物流问题,既可以指示相应的管理策略,又可以生成最佳的动态更新决策{ k*j } 。因此,管理决策者能够真正参与决策过程, 做到了“知其然, 亦知其所以然”。
上一篇:杨氏方程(第三章 混沌之美)
下一篇:杨氏方程(最终章 统一之美)
- 第十九次全国代表大会报告全文2017.10.18
- 中共十九大隆重开幕2017.10.18
- 新三板企业IPO热情高涨 11家已上2017.10.18
- 新一届发审委委员六大看点2017.10.12
- 人民币汇率升值与人民币贬值的两2018.06.15
- 杨氏方程(最终章 统一之美)2018.06.15
最新文章
-
百度料成搭乘CDR“首
中国证券报记者从知情人士处获悉......

-
中国人保IPO过会 拟
6月5日,证监会发审委召开第85次I......

-
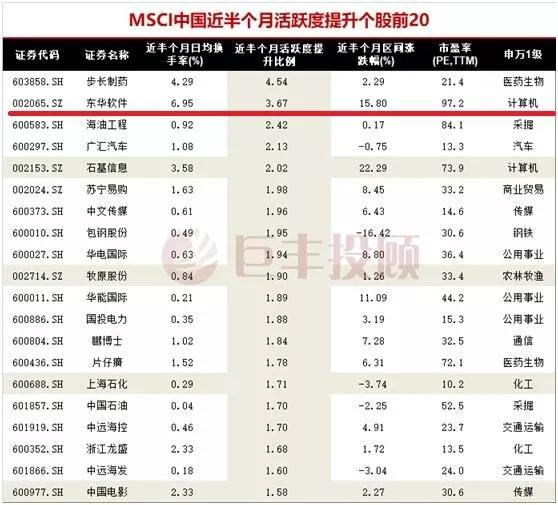
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......
-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

推荐文章
-
百度料成搭乘CDR“首
中国证券报记者从知情人士处获悉......

-
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......

-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

热门文章
-
阅读理解:看好看涨的
一般而言,相关个股被纳入指数后,......

-
东华助力永泰智慧化
2018年5月5日,福建省委常委、福州......

-
东华软件在2018数博
5月29日,2018中国国际大数据博览......